Skip to main content

Section 6.2 Using Definite Integrals to Find Volume

Just as we can use definite integrals to add the areas of rectangular slices to find the exact area that lies between two curves, we can also use integrals to find the volume of regions whose cross-sections have a particular shape.

In particular, we can determine the volume of a solid for which can be sliced into slabs for which the cross-sectional areas can be determined. The cross-secctional area multiplied by the thickness of the slab gives the volume of the slab. By adding up the volumes of these individual slices we get an approximation to the volume of the solid. The sum of the volumes is a Riemann sum, hence we may use the definite integral to calculuate the total volume of the solid. We first consider a familiar shape in Preview Activity 6.2.1: a circular cone.

Preview Activity 6.2.1.

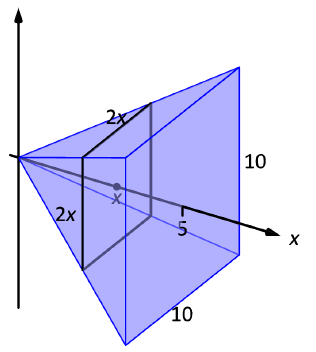
Consider a circular cone of radius 3 and height 5, which we view horizontally as pictured in Figure 6.2.1. Our goal in this activity is to use a definite integral to determine the volume of the cone.

Figure 6.2.1. The circular cone described in Preview Activity 6.2.1

  1. Find a formula for the linear function \(y = f(x)\) that is pictured in Figure 6.2.1.

  2. For the representative slice of thickness \(\Delta x\) that is located horizontally at a location \(x\) (somewhere between \(x = 0\) and \(x = 5\)), what is the radius of the representative slice? Note that the radius depends on the value of \(x\text{.}\)

  3. What is the volume of the representative slice you found in (b)?

  4. What definite integral will sum the volumes of the thin slices across the full horizontal span of the cone? What is the exact value of this definite integral?

  5. Compare the result of your work in (d) to the volume of the cone that comes from using the formula \(V_{\text{cone} } = \frac{1}{3} \pi r^2 h\text{.}\)

Subsection 6.2.1 The Volume by Slices

The solid in Figure 6.2.1 is a three dimensional solid whose cross-sections perpendicular to the \(x\)-axis are circles. The radius of each circle is the \(y\)-coordinate of the point on the line \(y=3-\frac{3}{5}x\) from \(x=0\) to \(x=5.\) If the interval from \(x=0\) to \(x=5\) is subdivided into \(n\) pieces of width \(dx=\frac{5}{n}\text{,}\) then each cross-sectional area is given by \(Area=\pi(3-\frac{3}{5}x)^2\text{.}\) The volume of each slab is \(\pi(3 - \frac{3}{5}x)^2\, dx.\) Adding all of the volumes produces a Riemann sum. We may use a definite integral to calculate the exact volume:

\begin{align*} \end{align*}

Figure 6.2.2. Volume of a General Slab

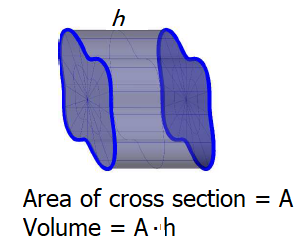
The volume of a general slab, as shown in Figure 6.2.2, is

\begin{equation*} \text{Area of the cross-section } \times \text{ thickness of the slab}. \end{equation*}

We can use this fact as the building block in finding volumes of a variety of shapes.

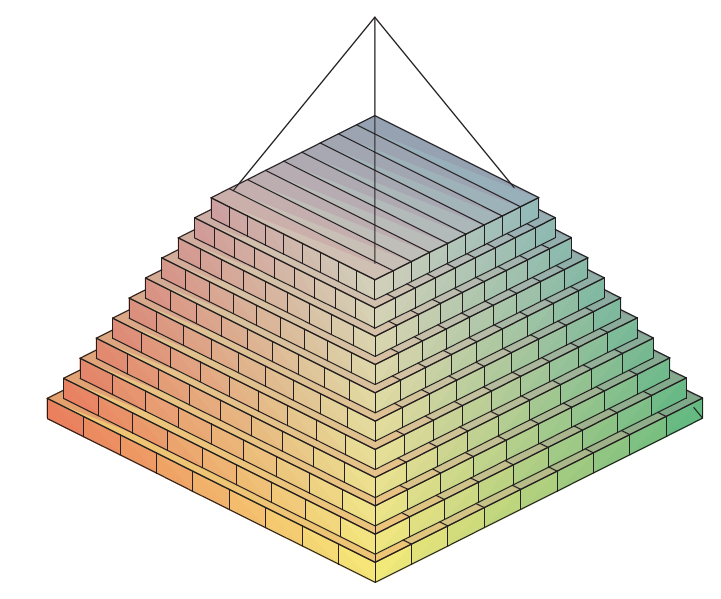
Given an arbitrary solid, we can approximate its volume by cutting it into \(n\) thin slices. When the slices are thin, each slice can be approximated by its cross-sectional area times the thickness of the slice.

By orienting a solid slong the \(x\)-axis, we can let \(A(x)\) represent the cross-sectional area of the \(i^{}\) slice, and let \(\Delta x_i\) represent the thickness of this slice (the thickness is a small change in \(x\text{.}\)) The total volume of the solid is approximately

\begin{equation*} \text{Volume} \approx \sum_{i=1}^n A(x_i)\Delta x_i. \end{equation*}

Recognize that this is a Riemann Sum. By taking a limit (as the thickness of the slices goes to \(0\)) we can find the volume exactly.

Volume By Cross-Sectional Area.

The volume \(V\) of a solid, oriented along the \(x\)-axis with cross-sectional area \(A(x)\) from \(x=a\) to \(b,\) is

\begin{equation*} V = \int_a^b A(x) \, dx. \end{equation*}

Find the volume of a pyramid with a square base of side length \(10\)in and a height of \(5\)in.

Solution
Figure 6.2.4. Orienting a pyramid along the \(x\)-axis

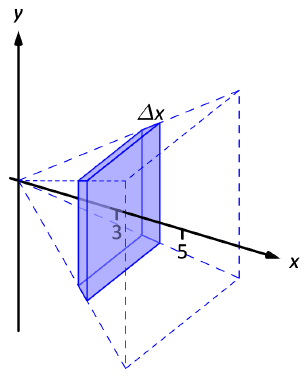
There are many ways to "orient" the pyramid along the \(x\)-axis; Figure 6.2.4 gives one such way, with the pointed top of the pyramid at the origin and the \(x\)-axis going through the center of the base.

We slice the solid into vertical slices of thickness \(\Delta x\) between \(x = 0\) and \(x = 5\text{.}\) Each cross section of the pyramid is a square. To determine its area \(A(x),\) we need to determine the side lengths of the square.

When \(x=5,\) the square has side length \(10.\) When \(x=0,\) the square has side length \(0.\) Since the edges of the pyramid are lines, we see that each cross-sectional slice has side length \(2x,\) giving \(A(x) = (2x)^2 = 4x^2.\)

Figure 6.2.5. A slice in the pyramid at \(x=3\) \(x=3\)

If one were to cut a slice out of the pyramid at \(x=3,\) as shown in (((Unresolved xref, reference "F-6-2-Ex3"; check spelling or use "provisional" attribute)))Figure , one would have a shape with square bottom and top with sloped sides. If the slice were thin, both the bottom and top squares would have sides lengths of about \(6\text{,}\) and thus the cross-sectional area is about \(36 ^2.\) Letting \(\Delta x\text{,}\) represent the thickness of the slice, the volume of this slice would then be about \(36\Delta x^3.\)

Cutting the pyramid into \(n\) slices divides the total volume into \(n\) equally-spaced smaller pieces, each with volume \((2x_i)^2\Delta x_i\text{,}\) where \(x_i\) is the approximaate location of the slice along the \(x\)-axis and \(\Delta x\) represents the thickness of each slice. One can approximate the total volume of the pyramid by summing up the volumes of these slices:

\begin{equation*} \text{Approximate volume} = \sum_{i=1}^n (2x_i)^2 \Delta x. \end{equation*}

Taking the limit as \(n \rightarrow \infty\) gives the actual volume of the pyramid; recognizing this sum as a Rieman Sum allows us to find the exact answer using a definite integral.

We have

\begin{align*} V \amp = \lim_{n \rightarrow \infty} \sum_{i=1}^n (2x_i)^2 \Delta x\\ \amp = \int_0^5 4x^2 \,dx\\ \amp = \left. \frac{4}{3}x^3 \, \right|_0^5\\ \amp = \frac{500}{3} \text{ in}^3. \end{align*}

We can check our work consulting the general equation for the volume of a pyramid:

\begin{equation*} V = \frac{1}{3} \times \text{ area of base } \times \text{height.} \end{equation*}

Certainly, using this formula from geometry is faster than our new method, but the calculus-based method can be applied to much more than just pyramids or cones.

We could determine the volume of the pyramid with a different definite integral if we orient it differently. Consider the same problem from a different point of view.

Once again, find the volume of a pyramid with a square base of side length \(10\)in and a height of \(5\)in.

Solution
Figure 6.2.7. Orienting a pyramid along the \(y\)-axis

This time we look at the pyramid with the base as shown in Figure 6.2.8 with the origin in the middle of the base and the \(y\)-axis going through the top. We slice the solid horizontally to make thin square slabs \(\Delta y\) thick between \(y = 0\) and \(y = 5\text{.}\) Each cross-sectional area, \(A(y),\) is determined by the length of its sides.

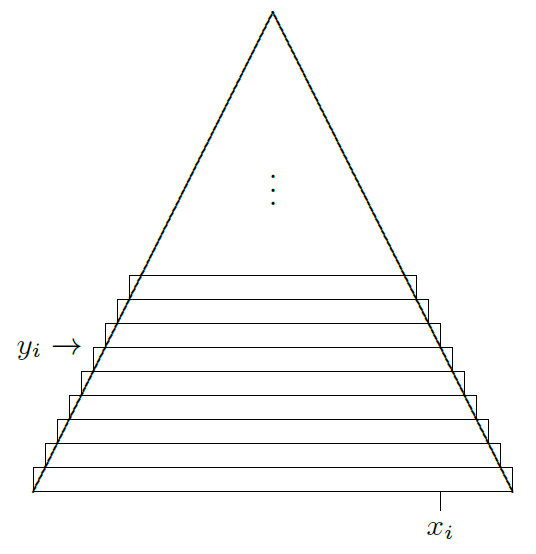
Figure 6.2.8. Horizontal slices of the pyramid

The length of a side is two times the distance from the \(y\)-axis to the line \(y=-x+5\text{.}\) Notice that this distance is the value of the \(x\)-coordinate of the point on the line where the slice touches the line: \(x=5-y\text{.}\) Each slice has volume \((2(5-y))^2 \Delta y= (10-2y)^2 \Delta y.\)

As in Example 6.2.3 the volumes of the slices are added to determine the total volume. Again, the exact volume will be given by the definite integral, but this integral will be in terms of \(y\) not \(x\text{.}\)

\begin{align*} V \amp = \int_0^5 (10-2y)^2 \,dy\\ \amp = \int_0^5 100-40y+4y^2 \,dy\\ \amp = \left. 100y - 20y^2 +\frac{4}{3}y^3 \, \right|_0^5\\ \amp = 100(5) - 20(5)^2 +\frac{4}{3}(5)^3 \\ \amp = \frac{500}{3} \text{ in}^3. \end{align*}

Hence, the way we set up the definite integral depends on how we orient the solid on an axis system.

Subsection 6.2.2 Summary

  • We can use a definite integral to find the volume of a three-dimensional solid by taking slices of the volume and adding up the volumes of the slices. The volume of a slice will be the cross-sectional area times the thickness of the slice.

  • If our slices are horizontal and of thickness \(\Delta y\) then the definite integral will be in terms of \(y.\) This leads us to integrate with respect to \(y\text{,}\) as opposed to with respect to \(x\) when we slice a solid vertically.

Exercises 6.2.3 Exercises

1. Solid of revolution from one function about the \(x\)-axis.
2. Solid of revolution from one function about the \(y\)-axis.
3. Solid of revolution from two functions about the \(x\)-axis.
4. Solid of revolution from two functions about a horizontal line.
5. Solid of revolution from two functions about a different horizontal line.
6. Solid of revolution from two functions about a vertical line.
7.

Consider the curve \(f(x) = 3 \cos(\frac{x^3}{4})\) and the portion of its graph that lies in the first quadrant between the \(y\)-axis and the first positive value of \(x\) for which \(f(x) = 0\text{.}\) Let \(R\) denote the region bounded by this portion of \(f\text{,}\) the \(x\)-axis, and the \(y\)-axis.

  1. Set up a definite integral whose value is the exact arc length of \(f\) that lies along the upper boundary of \(R\text{.}\) Use technology appropriately to evaluate the integral you find.

  2. Set up a definite integral whose value is the exact area of \(R\text{.}\) Use technology appropriately to evaluate the integral you find.

  3. Suppose that the region \(R\) is revolved around the \(x\)-axis. Set up a definite integral whose value is the exact volume of the solid of revolution that is generated. Use technology appropriately to evaluate the integral you find.

  4. Suppose instead that \(R\) is revolved around the \(y\)-axis. If possible, set up an integral expression whose value is the exact volume of the solid of revolution and evaluate the integral using appropriate technology. If not possible, explain why.

Answer

  1. \(L = \int_0^{1.84257} \sqrt{1+\left( -3 \sin \left(\frac{x^3}{4}\right) \cdot \frac{3}{4}x^2 \right)^2} \, dx \approx 4.10521\text{.}\)

  2. \(A = \int_0^{1.84527} 3 \cos\left( \frac{x^3}{4} \right) \, dx \approx 4.6623 \text{.}\)

  3. \(V = \int_0^{1.84527} \pi \cdot 9 \cos^2 \left( \frac{x^3}{4} \right) \, dx \approx 40.31965 \text{.}\)

  4. \(V = \int_0^3 \pi \left( 4\arccos \left(\frac{y}{3} \right) \right)^{2/3} \, dy \approx 23.29194 \text{.}\)

Solution

  1. Plotting the function and using technology to find where \(f(x)\) intersects the \(x\)-axis, we see that the region \(R\) as pictured in the following figure.

    To apply the formula we developed for arc length, we need the derivative of \(f\text{.}\) By the chain rule, \(f'(x) = -3 \sin(\frac{x^3}{4}) \cdot \frac{3}{4}x^2\text{,}\) so the arc length of \(f\) that lies along the upper boundary of \(R\) is

    \begin{equation*} L = \int_0^{1.84257} \sqrt{1+\left( -3 \sin \left(\frac{x^3}{4}\right) \cdot \frac{3}{4}x^2 \right)^2} \, dx\text{.} \end{equation*}

    Using technology to evaluate the integral, we find \(L \approx 4.10521\text{.}\)

  2. The area of \(R\) is

    \begin{equation*} A = \int_0^{1.84527} 3 \cos\left( \frac{x^3}{4} \right) \, dx \approx 4.6623\text{.} \end{equation*}

  3. Revolving \(R\) around the \(x\)-axis, we can use the disk method with slices perpendicular to the \(x\)-axis to find the volume of the resulting region. Noting that the radius of each such disk is \(r(x) = 3 \cos(\frac{x^3}{4})\) and the width of each such disk is \(\triangle x\text{,}\) we know the volume of each slice is

    \begin{equation*} V_{\text{slice}} \approx \pi r(x)^2 \triangle x = \pi \left( 3 \cos\left( \frac{x^3}{4} \right) \right)^2 \triangle x \end{equation*}

    and thus the total volume is

    \begin{equation*} V = \int_0^{1.84527} \pi \cdot 9 \cos^2 \left( \frac{x^3}{4} \right) \, dx \approx 40.31965 \end{equation*}

  4. If we instead revolve \(R\) around the \(y\)-axis, we need to use horizontal disks of thickness \(\triangle y\) in order to apply the disk method. To do that, we also need to express \(x\) as a function of \(y\text{,}\) rather than \(y\) as a function of \(x\) as given. Thus we take the given function \(y = 3 \cos(\frac{x^3}{4})\) and solve the equation for \(x\text{.}\) First, we observe

    \begin{equation*} \cos\left( \frac{x^3}{4} \right) = \frac{y}{3} \end{equation*}

    and thus using the inverse cosine,

    \begin{equation*} \frac{x^3}{4} = \arccos \left( \frac{y}{3} \right) \end{equation*}

    and therefore \(x^3 = 4\arccos \left(\frac{y}{3} \right)\) so that

    \begin{equation*} x = \sqrt[3]{4\arccos \left(\frac{y}{3} \right)}\text{.} \end{equation*}

    Now, a typical slice has radius \(r(y) = \sqrt[3]{4\arccos \left(\frac{y}{3} \right)}\) with thickness \(\triangle y\text{,}\) and volume

    \begin{equation*} V_{\text{slice}} \approx \pi \cdot \left( \sqrt[3]{4\arccos \left(\frac{y}{3} \right)} \right)^2 \triangle y\text{.} \end{equation*}

    Integrating to add up the slices from \(y = 0\) to \(y = 3\text{,}\) we have the volume of the solid of revolution is

    \begin{equation*} V = \int_0^3 \pi \left( 4\arccos \left(\frac{y}{3} \right) \right)^{2/3} \, dy \approx 23.29194\text{.} \end{equation*}
8.

Consider the curves given by \(y = \sin(x)\) and \(y = \cos(x)\text{.}\) For each of the following problems, you should include a sketch of the region/solid being considered, as well as a labeled representative slice.

  1. Sketch the region \(R\) bounded by the \(y\)-axis and the curves \(y = \sin(x)\) and \(y = \cos(x)\) up to the first positive value of \(x\) at which they intersect. What is the exact intersection point of the curves?

  2. Set up a definite integral whose value is the exact area of \(R\text{.}\)

  3. Set up a definite integral whose value is the exact volume of the solid of revolution generated by revolving \(R\) about the \(x\)-axis.

  4. Set up a definite integral whose value is the exact volume of the solid of revolution generated by revolving \(R\) about the \(y\)-axis.

  5. Set up a definite integral whose value is the exact volume of the solid of revolution generated by revolving \(R\) about the line \(y = 2\text{.}\)

  6. Set up a definite integral whose value is the exact volume of the solid of revolution generated by revolving \(R\) about the line \(x = -1\text{.}\)

Answer

  2. \(A = \int_0^{\frac{\pi}{4}} ( \cos(x) - \sin(x) ) \, dx \text{.}\)

  3. \(V = \int_0^{\frac{\pi}{4}} \pi (\cos^2(x) - \sin^2(x)) \, dx \text{.}\)

  4. \(V = \int_0^{\frac{\sqrt{2}}{2}} \pi \arcsin^2(y) \, dy + \int_{\frac{\sqrt{2}}{2}}^1 \pi \arccos^2(y) \, dy\)

  5. \(V = \int_0^{\frac{\pi}{4}} \pi [(2 - \sin(x))^2 - (2 - \cos(x))^2] \, dx \text{.}\)

  6. \(V = \int_0^{\frac{\sqrt{2}}{2}} \pi [ (1+\arcsin(y))^2 - 1^2 ] \, dy + \int_{\frac{\sqrt{2}}{2}}^1 \pi [ (1+\arccos(y))^2 - 1^2 ] \, dy\)

Solution

  1. See the sketch above. The exact intersection point of the curves is where \(\cos(x) = \sin(x)\) in the first quadrant, and thus at the point \((\frac{\pi}{4}, \frac{\sqrt{2}}{2})\text{.}\)

  2. The area of \(R\) is given by the definite integral

    \begin{equation*} A = \int_0^{\frac{\pi}{4}} ( \cos(x) - \sin(x) ) \, dx\text{.} \end{equation*}

  3. Revolving \(R\) about the \(x\)-axis and using slices perpendicular to the axis with thickness \(\triangle x\text{,}\) the outer radius of the resulting washers is \(R(x) = \cos(x)\text{,}\) while the inner radius of the washers is \(r(x) = \sin(x)\text{.}\) The volume of a typical slice is

    \begin{equation*} V_{\text{slice}} \approx \pi (\cos^2(x) - \sin^2(x)) \triangle x \end{equation*}

    and thus using an integral to sum the slices over the interval \(x = 0\) to \(x = \pi/4\text{,}\) we find the volume of the solid is

    \begin{equation*} V = \int_0^{\frac{\pi}{4}} \pi (\cos^2(x) - \sin^2(x)) \, dx\text{.} \end{equation*}

  4. Revolving \(R\) about the \(y\)-axis, the resulting figure has solid cross sections that are disks perpendicular to the \(y\)-axis with thickness \(\triangle x\text{,}\) but the radius \(R(y)\) that governs the radius of each disk changes at the height where \(y = \frac{\sqrt{2}}{2}\) in the interval from \(y = 0\) to \(y = 1\text{.}\) We also need to express the two curves that bound the region with \(x\) as a function of \(y\text{.}\) On the interval from \(y = 0\) to \(y = \frac{\sqrt{2}}{2}\text{,}\) the sine function provides the boundary, which we write as \(x = \arcsin(y)\text{;}\) on the interval from \(y = \frac{\sqrt{2}}{2}\) to \(y = 1\text{,}\) the cosine function provides the boundary, which we write as \(x = \arccos(y)\text{.}\) On the lower interval, a typical slice has volume

    \begin{equation*} V_{\text{slice}} \approx \pi \arcsin^2(y) \triangle y\text{.} \end{equation*}

    Using similar reasoning for the upper interval and summing the slices using appropriate definite integrals, we find that

    \begin{equation*} V = \int_0^{\frac{\sqrt{2}}{2}} \pi \arcsin^2(y) \, dy + \int_{\frac{\sqrt{2}}{2}}^1 \pi \arccos^2(y) \, dy \end{equation*}

  5. Draw a picture. Revolving \(R\) about the line \(y = 2\text{,}\) we see that cross-sections perpendicular to the line \(y = 2\) are washers with thickness \(\triangle x\text{,}\) outer radius \(R(x) = 2 - \sin(x)\text{,}\) and inner radius \(r(x) = 2 - \cos(x)\text{,}\) since \(2 - \sin(x) \ge 2 - \cos(x)\) on the interval \([0, \frac{\pi}{4}]\text{.}\) Thus, the volume of a typical slice is

    \begin{equation*} V_{\text{slice}} \approx \pi [(2 - \sin(x))^2 - (2 - \cos(x))^2] \triangle x \end{equation*}

    and hence integrating to sum the total volume, we find

    \begin{equation*} V = \int_0^{\frac{\pi}{4}} \pi [(2 - \sin(x))^2 - (2 - \cos(x))^2] \, dx\text{.} \end{equation*}

  6. Revolving \(R\) about the line \(x = -1\text{,}\) the resulting figure has solid cross sections that are washers perpendicular to the \(y\)-axis with thickness \(\triangle x\text{;}\) the inner radius is always \(r(y) = 1\text{,}\) but the outer radius \(R(y)\) that governs the larger radius of each washer changes at the height where \(y = \frac{\sqrt{2}}{2}\) in the interval from \(y = 0\) to \(y = 1\text{.}\) As in (d), we express the two curves that bound the region with \(x\) as a function of \(y\text{.}\) On the interval from \(y = 0\) to \(y = \frac{\sqrt{2}}{2}\text{,}\) \(R(y) = 1 + \arcsin(y)\text{;}\) on the interval from \(y = \frac{\sqrt{2}}{2}\) to \(y = 1\text{,}\)\(R(y) = 1 + \arccos(y)\text{.}\) On the lower interval, a typical slice has volume

    \begin{equation*} V_{\text{slice}} \approx \pi [ (1+\arcsin(y))^2 - 1^2 ] \triangle y\text{.} \end{equation*}

    Using similar reasoning for the upper interval and summing the slices using appropriate definite integrals, we find that

    \begin{equation*} V = \int_0^{\frac{\sqrt{2}}{2}} \pi [ (1+\arcsin(y))^2 - 1^2 ] \, dy + \int_{\frac{\sqrt{2}}{2}}^1 \pi [ (1+\arccos(y))^2 - 1^2 ] \, dy \end{equation*}
9.

Consider the finite region \(R\) that is bounded by the curves \(y = 1+\frac{1}{2}(x-2)^2\text{,}\) \(y=\frac{1}{2}x^2\text{,}\) and \(x = 0\text{.}\)

  1. Determine a definite integral whose value is the area of the region enclosed by the two curves.

  2. Find an expression involving one or more definite integrals whose value is the volume of the solid of revolution generated by revolving the region \(R\) about the line \(y = -1\text{.}\)

  3. Determine an expression involving one or more definite integrals whose value is the volume of the solid of revolution generated by revolving the region \(R\) about the \(y\)-axis.

  4. Find an expression involving one or more definite integrals whose value is the perimeter of the region \(R\text{.}\)

Answer

  1. \(A = \int_0^{1.5} 1+\frac{1}{2}(x-2)^2 - \frac{1}{2}x^2 \ dx = 2.25\text{.}\)

  2. \(V = \int_0^{1.5} \pi\left[\left(2+\frac{1}{2}(x-2)^2\right)^2 - \left(1+\frac{1}{2}x^2\right)^2 \right] \ dx = \frac{315}{32} \pi\)

  3. \(V = \int_{0}^{1.125} \pi \left(\sqrt{2y}\right)^2 \ dy + \int_{1.125}^3 \pi \left(2 - \sqrt{2(y-1)}\right)^2 \ dy \approx 7.06858347 \text{.}\)

  4. \(P = 3 + \int_0^{1.5} \sqrt{1+(x-2)^2} + \sqrt{1+x^2} \ dx \approx 7.387234642 \text{.}\)

Solution

  1. A picture of the region is shown in the figure above. The point of intersection occurs when

    \begin{equation*} 1+\frac{1}{2}(x-2)^2 = \frac{1}{2}x^2\text{,} \end{equation*}

    so \(2+(x-2)^2 = x^2\text{,}\) which implies \(2+(x^2-4x+4) = x^2\) and thus \(4x=6\) so \(x = \frac{3}{2}\text{.}\) Since \(g(x) = 1+\frac{1}{2}(x-2)^2 \ge \frac{1}{2}x^2 = f(x)\) on the interval \(\left[0, \frac{3}{2} \right]\text{,}\) the area of the region between the two curves is

    \begin{align*} A = &= \int_0^{1.5} 1+\frac{1}{2}(x-2)^2 - \frac{1}{2}x^2 \ dx\\ &= \int_0^{1.5} 1+\frac{1}{2}(x^2-4x+4) - \frac{1}{2}x^2 \ dx\\ &= \int_0^{1.5} 3-2x \ dx\\ &= \left(3x-x^2\right)\biggm|_{0}^{1.5}\\ &= 4.5-2.25\\ &= 2.25\text{.} \end{align*}

  2. (You should draw a picture of the solid, based on the figure above, with the region \(R\) revolved about \(y = -1\text{.}\)) We slice vertically so that our cross sections are washers with thickness \(\triangle x\text{.}\) Because we are revolving about \(y = -1\text{,}\) the outer radius is \(R(x) = 2+\frac{1}{2}(x-2)^2\text{,}\) while the inner radius is \(1+\frac{1}{2}x^2\text{.}\) Hence the volume of a typical slice, which has thickness \(\triangle x\) is given by

    \begin{equation*} V_{\text{slice}} \approx \pi \left( R(x)^2 - r(x)^2 \right) \triangle x = \pi\left[\left(2+\frac{1}{2}(x-2)^2\right)^2 - \left(1+\frac{1}{2}x^2\right)^2 \right] \triangle x\text{.} \end{equation*}

    Hence, the volume of the solid obtained by revolving the region \(R\) around the line \(y=-1\) is given by

    \begin{equation*} V = \int_0^{1.5} \pi\left[\left(2+\frac{1}{2}(x-2)^2\right)^2 - \left(1+\frac{1}{2}x^2\right)^2 \right] \ dx = \frac{315}{32} \pi \end{equation*}

  3. (Draw a picture of the solid, based on revolving the region \(R\) about the \(y\)-axis.) We slice horizontally and thus the resulting cross sections are cylinders with thickness \(\triangle y\text{.}\) The radius of the disks changes as \(y\) passes through \(f\left(\frac{3}{2}\right) = \frac{9}{8} = 1.125\text{,}\) so we need two different integrals to find the total volume. Since we are slicing horizontally, we will integrate with respect to \(y\text{,}\) so we need to solve both of our equations for \(x\) as functions of \(y\text{.}\) Observe that \(y = 1+\frac{1}{2}(x-2)^2 \) implies \(2(y-1) = (x-2)^2\text{,}\) so \(x-2 = \pm \sqrt{2(y-1)}\) and thus \(x = 2 \pm \sqrt{2(y-1)}\text{,}\) and similarly \(y = \frac{1}{2}x^2\) implies \(x = \pm \sqrt{2y}\text{.}\) The portion of the curve defined by \(y = 1+\frac{1}{2}(x-2)^2\) that determines one of the boundaries is the left hand portion of the parabola, so \(x = 2 - \sqrt{2(y-1)}\text{,}\) while the portion of the curve \(y = \frac{1}{2}x^2\) that determines the other boundary is the right hand portion of the parabola, so \(x = \sqrt{2y}\text{.}\) These two curves define the radius of the disk (one for \(y \lt 1.125\text{,}\) the other for \(y \gt 1.125\)) and the lowest point on the region is \((0,0)\) while the highest is \((0,3)\text{.}\) So a sum of integrals that represents the volume of the solid obtained by revolving the region \(R\) around the \(y\)-axis is

    \begin{equation*} V = \int_{0}^{1.125} \pi \left(\sqrt{2y}\right)^2 \ dy + \int_{1.125}^3 \pi \left(2 - \sqrt{2(y-1)}\right)^2 \ dy \approx 7.06858347 \end{equation*}

  4. Recall that the length of a curve defined by a function \(f\) on an interval \([a,b]\) is given by

    \begin{equation*} \int_a^b \sqrt{1+(f'(x))^2} \ dx\text{.} \end{equation*}

    To find the perimeter of the region \(R\) we calculate the length of the curves defined by \(y = 1+\frac{1}{2}(x-2)^2\) (for which \(y' = x-2\)) and \(y=\frac{1}{2}x^2\) (for which \(y' = x\)) on the interval \([0,1.5]\) and the length of the segment along \(x=0\) as \(y\) goes from \(0\) to \(3\text{.}\) This last length is \(3\text{,}\) so the perimeter of the region \(R\) is given by

    \begin{equation*} P = 3 + \int_0^{1.5} \sqrt{1+(x-2)^2} + \sqrt{1+x^2} \ dx \approx 7.387234642\text{.} \end{equation*}
login